TARTAGLIA TRIANGLE.

So, there I'm going to talk about the Triangle Tartaglia.

• The triangle Tartaglia combinatorial numbers or Pascal (because it was the mathematician who popularized it) is a triangle of integers, infinite and symmetric.
• Pascal's triangle Tartaglia will be very useful for calculating the Newton's binomial coefecientes. (Formula which provides development nth power of n -n being positive integer- of a binomial.)
• It is associated with the name of the mathematician Pascal because he wrote the first treatise of the triangle and Tartaglia because the italian, was the first who published it in Europe.

                  

• The properties of this triangle were known many years before Pascal formulate, by chinese, indian, persian mathematicians ... but it was he who organized all the information together.

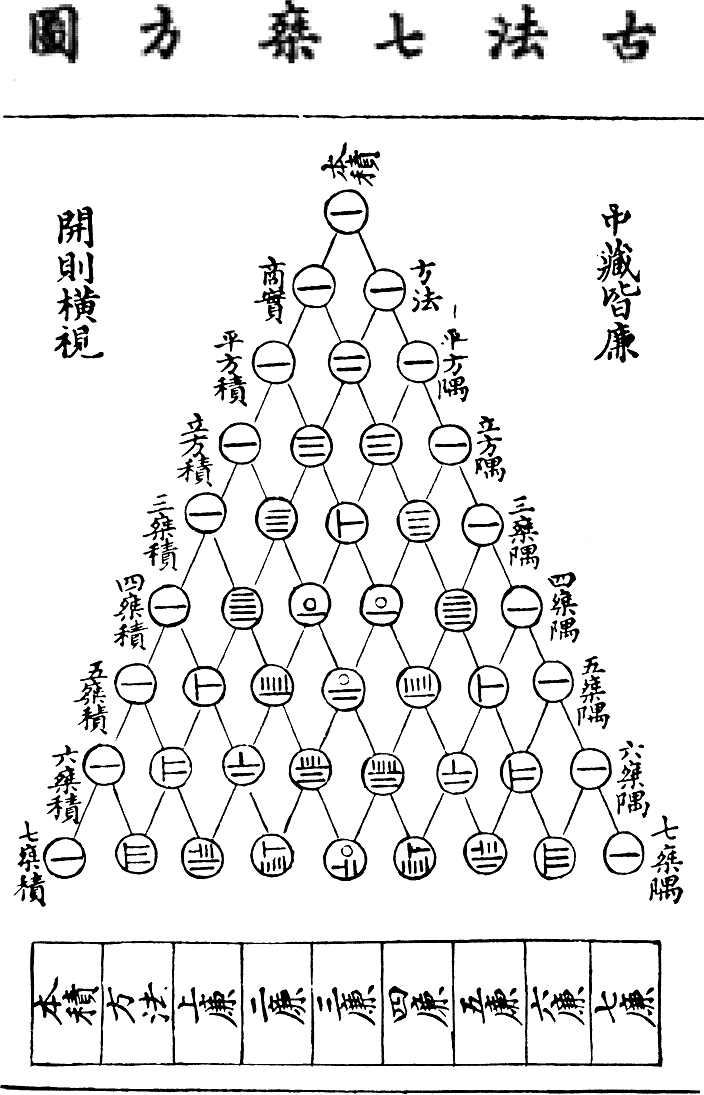
          For example, in China there isn't Pascal's triangle, there is Yang Hui's triangle. (You can see it at the picture below.)

                           

• The construction of the Tartaglia triangle is like that and following:

                            

• Some numbers, such as - 1 2 1 - y - 1 3 3 1 - are the coefficients of the identities below:

         (a + b)² = a² + 2 · a · b + b²

        (a + b)³ = a³ + 3 · a² · b + 3 · a · b² + b³

Mathematics in real life.

Now, I'm going to talk about mathematics in real life. Nowadays, a big number of students think that maths will not appeared in their futures, that maths won't be a problem because of the advances in technology, or the uses of calculators, but they're wrong. Maths is in every step we take, because every day we should resolve many numeral problems in each situation.

We can use Maths in situations such us:

When we are doing the shopping, when they look for the lowest price, or calculating the discount that are marked; In the kitchen, when we make a recipe, changing the units of measurement; With the money, when you calculate the amount of money that the other have to give you, or to count the coins that you need to buy a product; In trips, to calculate the estimated time of arrival...

This are many situations in life that required the use of the mathematics, so I think that we have to learn it for the best in our future, as you can see, every single day we use it!

INTRODUCTION.

• This blog has been created with the goal of learning, is a way to learn about the subjects of Calculus, Algebra and Communication skills in engineering and create a blog.
• This entry will address a specific topic, calculus.
• Calculus refers to the result for the action to calculate or count. Calculate, is to perform the operations necessary to predict the outcome or know the consequences of a previously known data. 

                 - The most common use of the term calculation is the logical-mathematical. From this perspective, the calculation is a mechanical process where we know the consequences of a previously known data.

                 - The calculation is natural for human when we start to relate things together, in logical-mathematical sense appears when reason begins to formalize.

• Today we can say that the calculus is a binary system, which has great computing power achieved by computers, its calculation speed is inhuman, millions of operations per second.